Point-particle explanations: the case of gravitational waves

A highly idealized model of a physical system contains key components and dependency relations that do not represent elements of the system itself. In some cases, these elements of the model may nonetheless be used to explain phenomena or regularities in the physical system—or so philosophers have claimed. Robert Batterman, for instance, has explored the use of infinite idealization to explain the universality of structural features in hydrodynamics and thermodynamics. The claim is that asymptotic analyses, which systematically abstract away from micro details, enable idealized models to explain underlying structural or universal features (Batterman 2002, 2005; Batterman and Rice 2014). Alisa Bokulich has suggested that “fictional models,” such as semi-classical models, can be explanatory if they meet certain conditions (Bokulich 2011; Bokulich, 2012). Richard Healey offers detailed accounts of explanations from quantum theory, demonstrating that the explanatory elements of quantum models do not play any representational role (Healey 2015).

This paper investigates explanatory practices in general relativity (GR), and in particular explanations of gravitational waves using models that contain point-particle idealizations. The point-particle assumption, that there is a finite mass contained in an infinitesimal volume, is not physically realistic. Physical point-particle sources simply cannot exist, according to GR. In this way, point particles in GR are similar to the infinite number of particles in a thermodynamic model at criticality or electrons with definite trajectories in a semi-classical model: not just an idealization, in the sense that the component of the model does not accurately represent an entity in the target system, but a physically impossible idealization according to our best relevant theory.

The goal of this paper is to explore the role of physically impossible idealizations in model-based explanation. We do this by examining the explanation of gravitational waves from distant stellar objects (Sect. 2). What makes this case interesting is that there are two very different kinds of models used for predicting the same gravitational wave phenomena, post-Newtonian (PN) models and effective field theory (EFT) models (Sect. 3). The paper contends that the former are explanatory while the latter are not. More precisely, the difference in the explanatory power of the two kinds of models is due to the differing roles physically impossible idealizations play (Sect. 4). In post-Newtonian models, point particles are not essential to the explanation; while they have not been eliminated from the models used to predict gravitational waves, we have good reason to believe they are eliminable in principle. By contrast, point particles (and other physically impossible idealizations) are essential elements of effective field theory models, and ineliminable from EFT predictions of gravitational waves (Sect. 5). The argument relies on a principle, developed and defended in Sect. 6, that a necessary condition for an idealized model to be explanatory is that no entity in the model that is essential to the explanation be physically impossible according to the relevant global theory.

Soon after formulating GR, Albert Einstein predicted the possibility of gravitational waves: short-wavelength perturbations of the spacetime metric approximating plane waves. Einstein developed a quadrupole radiation model and a Newtonian approximation in which the velocities of the bodies are infinitely small compared to the velocity of light (Einstein and Rosen 1937; cf. Landau and Lifshitz 1971). Heinrich Lorentz had already derived the first relativistic or post-Newtonian corrections to the equations of motion of bodies in GR (Lorentz and Droste 1917/1937). However, it was not until the 1960s that gravitational waves and relativistic dynamics were combined, and derivations of gravitational waves based on first-order post-Newtonian dynamics were systematically explored (Peters and Mathews 1963). Only since work in the mid-1980’s by Luc Blanchet and collaborators has the field of gravitational physics begun to produce accurate, quantitative models of gravitational waves emitted from realistic astronomical sources Blanchet (2014) provides a comprehensive review. As we shall see in outline, the problem is exceedingly difficult to solve.

One of the simplest sources of gravitational waves is an isolated system consisting of two compact astronomical bodies, such as black holes or neutron stars, approximately equal in mass. In systems of experimental interest, the two bodies spiral inward toward each other, the bound orbit slowly decays, and the two bodies coalesce over a timespan of the order of minutes. Energy is carried outward by gravitational waves, which in some cases may be detectable from Earth (Fig. 1). Gravitational waves provide astronomy with a powerful new way to probe distant parts of the galaxy and observe exotic new phenomena. Electromagnetic radiation couples strongly to charged matter, making it easy to detect but also easily scattered by intervening matter. By contrast, gravitational radiation couples very weakly to matter, which means it can travel over much larger distances. Over the last two decades, a number of detectors have been built to detect gravitational waves, including the Laser Interferometer Gravitational-wave Observatory (LIGO) in the US. LIGO detected the first gravitational waves from inspiral systems in September, 2015 (Collaboration and Virgo 2016).

Open image in new window

Figure 2 shows the basic building blocks of the two-body inspiral model. In this model the masses \(m_{1}\) and \(m_{2}\) are about equal, the bodies are on the order of \(r_{S}\) in diameter, and they orbit around each other in a roughly circular orbit on the order of distance d apart. Charge, spin and forces other than gravity are neglected. The model assumes that the velocities of the bodies are low, \(v/c<< 1\) and that the bodies are weakly self-gravitating. A key feature of the model is the distinction between the near zone and far zone regions of spacetime. Given a typical relative velocity v of the objects, the frequency of the binary system and the frequency of the corresponding gravitational waves will be on the order of v/d. The characteristic wavelength of the gravitational waves is thus \(\uplambda \sim d(c/v)\), where c is the speed of light. The near zone is characterized as the region in which the distance from the centre of the binary system is \(r<< \uplambda \). In this zone retardation effects can be neglected and the perturbation of the metric can be approximated by terms of an instantaneous potential. In the far zone, which is characterized by \(r> > \uplambda \), retardation effects are important and boundary conditions must be imposed. The near zone and far zone overlap in the buffer region. For concreteness, typical values may be \(r_{S} \approx 1\) km and \(d \approx 100\) km apart. The characteristic wavelength \(\uplambda \) of gravitational radiation thus ranges from the order of \(10^{5}\) km near the beginning of the inspiral to 10 km near coalescence.

Open image in new window

It is impossible in such an inspiral system to find an exact solution of the Einstein field equations (EFEs), the 10 coupled non-linear differential equations that express the laws of GR. So approximation methods are used. The starting point for early work on gravitational waves was the idea, based on an analogy with classical electrodynamics, of employing different approximation schemes at different length scales. As noted above, in the near zone retardation effects can be neglected, and the perturbation of the metric can be approximated by terms of an instantaneous potential. In the far zone, plane gravitational waves and retardation effects dominate. Again by analogy with electrodynamics, the strategy is to construct a uniformly valid approximation model using matching techniques at the overlap of the near and far zones, along with an appropriate choice of boundary and gauge conditions.

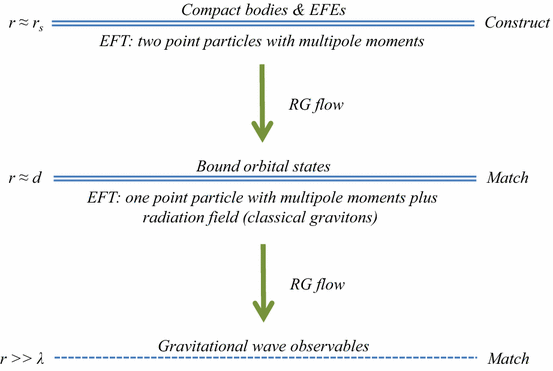
There are two distinct routes to constructing inspiral models that yield testable predictions: the post-Newtonian approximation and the effective field theory approach. The post-Newtonian approximation makes central use of singular perturbation theory to match the near-zone and far-zone models in the buffer region. This provides a consistent and theoretically justified method of obtaining a uniformly valid approximation of the gravitational radiation for a given order in the perturbation parameter. Similar predictions have been obtained using effective field theory methods imported into gravitational physics from the fields of particle physics and statistical mechanics. On the EFT approach, the gravitational field is modeled as a set of three distinct effective fields at distinct length scales, which are matched at their overlaps.

The term “post-Newtonian” in fact refers to a collection of interconnected models, theoretical assumptions and techniques developed and refined over several decades of work in gravitational physics. Strictly speaking, only the near zone is treated with a post-Newtonian (\(\hbox {PN}_{\mathrm{near}})\) approximation: ignore retardation effects, assume a weak gravitational field and slow velocities, and construct an approximate model of the gravitational potential that yields convergent (finite) results. The far zone consists of a model of gravitational waves on a post-Minkowski \((\hbox {PM}_{\mathrm{far}})\) expansion that takes into account boundary conditions at infinity. These are essentially plane wave perturbations on what is assumed outside the source (\(r > d)\) to be an approximately flat background metric. The goal is to obtain a uniformly valid solution by matching the \(\hbox {PN}_{\mathrm{near}}\) and \(\hbox {PM}_{\mathrm{far}}\) approximations in the buffer zone, given knowledge of the source and well-justified assumptions about large-scale spacetime structure and boundary conditions (Maggiore 2007; cf. Blanchet 2014 and references therein). We follow standard usage in calling all these elements together a post-Newtonian model. Post-Newtonian models yield surprisingly precise values for predictions of observable far-zone gravitational-wave phenomena. Indeed, as one well-known review puts it, these inspiral models and gravitational wave predictions are “[p]ossibly the most remarkable example of the unreasonable effectiveness of post-Newtonian theory” (Will 2011, p. 6).

Appendix A provides an overview of the construction of the PN model and the derivation of gravitational wave predictions based upon it. PN models begin with a version of the fundamental equations of GR, the relaxed EFEs. A \(\hbox {PM}_{\mathrm{far}}\) approximation constructs valid solutions of the EFEs in the far zone, where spacetime is void of matter and retardation effects are significant. A \(\hbox {PN}_{\mathrm{near}}\) approximation gives solutions of the relaxed EFEs valid in the near zone with two compact matter sources, the inspiralling bodies. Both approximations involve singular expansions, and regularization techniques are needed to eliminate the divergences. The two approximations are matched to create a model valid everywhere. As described in Appendix A, the point particle idealization is a key building block of the model.

Post-Newtonian models are referred to as \(n\hbox {PN}\) models, where n is the approximation order of the model. The far-zone gravitational waveform has been calculated up to order 3.5PN (Blanchet 2014, p. 93). Computation of the phase of gravitational waves at this order is sufficient to obtain predictions about the time evolution of gravitational wave phase observables, exactly the observables the LIGO detector has recently measured. In principle, the post-Newtonian approach provides a uniformly valid approximation of the metric for any given order. In practice, computations quickly become intractable beyond 4PN. Above 4PN, regularization techniques require unknown parameters and have other technical problems that render the results ambiguous (see Appendix A). Until recently, the 4PN model required several unknown parameters. These regularizations were improved by using dimensional regularization techniques imported from quantum field theory. But ambiguities and unknown coefficients persist above 4PN.

In 2006, Ira Goldberger and Walter Rothstein published a landmark paper developing the EFT approach to gravitational physics (Rothstein and Goldberger 2006). Goldberger and Rothstein took methods, assumptions, and intuitions from the effective field theory program in perturbative quantum field theory and applied them to gravitational physics, with astonishingly successful results. They developed an EFT model of binary inspiral systems, and they were able to re-derive the PN results for leading-order features of gravitational waves emitted by the system. Since then, the EFT approach has successfully modeled higher-order terms for binary inspiral systems using a fraction of the time and effort it took using PN models. A great advantage of the EFT approach to gravitational physics is that it makes use of familiar tools and methods from particle physics. However, significant disanalogies between particle physics and gravitational physics mean that the use of these tools requires additional theoretical justification in the gravitational context, justification that has not yet been supplied in several key places. The mathematical analogies between the two cases hide deep interpretive and—our focus here—explanatory differences.

In particle physics, one can construct a quantum field theory model of a physical system of interest, based on the most general Lagrangian consistent with certain constraints and symmetries, and this model will yield predictions for observable phenomena of interest in the form of an S-matrix. The model does not represent or correspond to actual particles and fields in the physical system (so it is not “fundamental”) but rather contains effective particles and fields that yield the right predictions for the physical system, at least in a limited domain to which the model applies. This approach in particle physics goes back to the origins of quantum field theory and Fermi’s model of weak interactions, and it has been especially influential since Weinberg’s work in the 1980s (Weinberg 1979; Hartmann 2001). The effective field theory approach to inspiral systems is based on an analogy with the use of effective field theories in particle physics. Unlike in particle physics, the EFTs used in gravitational physics are classical field theories, in which particles have definite worldlines and follow classical trajectories. As well, while in particle physics the main application of EFTs is to scattering problems, in gravitational physics there is no S-matrix picture and the focus is on time-dependent theory.

By analogy with the methods of quantum field theory, the first step in constructing an EFT model is to identify elements, the relevant degrees of freedom, and symmetries that the model should contain. The idea is to construct general equations of motion for the model that includes both particle dynamics and radiation modes of gravitational waves, consistent with these degrees of freedom and these symmetries. In fact, the EFT approach works, not with the equations of motion themselves, but with the effective action. Using the effective action greatly simplifies calculations by doing them at the level of the action functional and using Feynman rules to calculate path integrals. The effective action yields predictions about observables, such as far-zone gravitational wave phenomena.

The EFT model is constructed by writing GR in terms of an effective action integral, which is the sum of the Einstein–Hilbert action, encoding information about the EFEs, and a point-particle action, encoding features of the inspiralling bodies. The EFT takes advantage of separation of scales and uses renormalization group techniques to integrate out shorter-range physics. In a nutshell, the strategy is to construct an effective action for an effective field at each scale and match coefficients at the boundaries. The process is illustrated schematically in Fig. 3 and described in more detail in Appendix B.

Open image in new window

Since its development in 2006, the EFT approach has been able to reproduce results that took decades to obtain using traditional post-Newtonian methods. The EFT approach has successfully modeled higher-order corrections for binary inspiral system up to 4PN (Foffa and Sturani 2013). Moreover, according to proponents, it is poised to go well beyond the predictive accuracy and scope of traditional PN models.

From a calculational perspective, we are just lucky that the sorts of systems producing the gravitational waves we are interested in happen to be systems in which the point-particle approximation is predictively accurate. Mathematically, the concept of a point particle is well defined in terms of a delta-function distribution. As described in Sect. 2, due to the nonlinear nature of the EFEs, distributional (point-particle) sources cannot be used in the same straightforward way they can be used in linear theories like electromagnetism. Physicists have developed a well-defined procedure in GR to “shrink down” an extended body, letting its size and mass go to zero uniformly, in order to obtain a point-particle solution in certain situations. For instance, they have obtained a far-zone solution for the metric using a point-particle matter source that is approximately the same solution one obtains using a realistic extended-body matter source, and this is true independently of facts about the body (Gralla and Wald 2008). Indeed, point particles are particularly calculationally effective in the inspiral case we are considering. It turns out that even in the near zone, corrections to the calculations due to the finite size of the bodies do not appear until 5PN, a higher order than current PN calculations (Blanchet 2014, pp. 11–12). The reason is that the extended bodies here are black holes or neutron stars, small and rigid objects in which tidal effects are small. Larger and less rigid bodies, such as white dwarf stars, have greater tidal effects and corrections to the point-particle idealization come in at a lower order of approximation.

Point particles are physically impossible in GR, in the sense that they are not nomologically possible according to the laws of GR, the Einstein Field Equations. Point particles in GR are thus physically impossible idealizations in the same way as are an infinite number of particles in a thermodynamic model at criticality or electrons with definite trajectories in a semi-classical model. What distinguishes these physically impossible idealizations from garden-variety physically possible but non-actual idealizations? On the simplest view, the laws of a theory determine physically (nomologically) possible systems, in the sense that they impose dynamical constraints the possible ways physical systems can evolve, the relations between states at different times; contingent initial conditions then pick out a particular evolution for a given system. In contemporary physics, at least, the simplest view is wrong: the laws of a theory constrain physically possible initial conditions as well. Maxwell’s equations, for instance, provide not only dynamic but also synchronic constraints on physically possible electromagnetic systems (Frisch 2004). They do this by stipulating eight independent conditions as constraints, while the electromagnetic field has six degrees of freedom. In short, a physically possible idealization is one which is consistent with the dynamic and synchronic constraints of the relevant theory—think of point particles in electromagnetism, or a frictionless inclined plane in Newtonian mechanics. A physically impossible idealization is one which is inconsistent with relevant theory, including various infinite idealizations and, or focus here, point particles in GR.

That there are no massive objects of size zero is a synchronic constraint on the physically possible states in GR. A massive object of size zero might be thought of as some kind of singularity, but it is different in kind from a physical singularity such as a black hole. Black holes are obtained by a physical process of gravitational collapse that results in a coherent object with physical properties—it may be charged or spinning, for example—and with a finite radius. Point particles, by contrast, do not have well-defined physical properties at all in GR.

To see this point another way, consider the contrast with classical electromagnetism. In electromagnetism, point particles are both mathematically and physically unproblematic. As noted in Sect. 2, there is a straightforward mathematical treatment of delta-function charge-current sources. Physically, the basic entity of the theory is a point charge, and the fundamental equations of motion refer directly to point particles. In GR, point particles are also mathematically tractable, although not as easily as in electromagnetism. Distributional sources such as point particles can be used in the equations of motion of electromagnetism straightforwardly, while in GR distributional sources require additional assumptions and mathematical procedures to obtain unambiguous results. However, point particles are physically impossible according to GR, in stark contrast with electromagnetism. I suggest that our intuitions, based on over a century of working with Maxwell’s equations, can lead us astray in the context of a GR. This, coupled with the “unreasonable” and “surprising” calculational successes of PN models, may lead us to accept that a point-particle source distribution is physically realistic in GR when we should not.

Let us examine the very different roles the point-particle idealization plays in PN and EFT models in order to evaluate the models’ explanatory merits. PN models begin with the assumption that matter sources are discrete, or more precisely that the system has only a compact region of spacetime with non-zero stress-energy values. This assumption is physically realistic in a two-body inspiral system, because the two neutron stars or black holes are the only non-zero regions. Later on in the process, the construction of the \(\hbox {PN}_{\mathrm{near}}\) approximation requires the further constraint of point-particle sources, or in other words that the stress-energy tensor is nonzero at only two points. Point-particles come into PN models as a mathematical technique to obtain finite higher-order predictions. By contrast, point particles are essential and ineliminable in all EFT models, whether in gravitational physics, quantum field theory or condensed matter physics.

In principle, the post-Newtonian approach does not require point particles; all it requires is that the non-zero regions of the stress-energy tensor have compact support. In practice, in order to do higher-order calculations the \(\hbox {PN}_{\mathrm{near}}\) model assumes that the stress-energy tensor is nonzero only at two points, corresponding to the centres of mass of the two compact bodies (Appendix A). While physicists may not yet be able to eliminate the idealization from 4PN models of the sort described above, I contend that there are good reasons to believe that point particles are not essential to PN models.

A key point here is the effacement of internal structure in GR. It is a well-known fact about Newtonian gravitational theory that one can replace a model of the internal structure of the source with a model in which the gravitational field is defined over a surface outside the source. Internal structure is not relevant, and equations of motion defined over surface integrals are completely satisfactory. This effacement principle holds in GR as well. Einstein and collaborators derived post-Newtonian equations of motion in GR using surface integrals, where the resulting equations are applicable to any compact body (Einstein and Infeld 1938). The effacement principle allows us to say that in principle the same results obtained from a point-particle model would be obtained if, counterfactually, there were a calculationally tractable higher-order PN model with extended bodies.

Is it likely or even possible that such an extended-body model could ever be constructed? Building higher-order PN models containing extended bodies is a challenging task, and, as we have seen, one with no predictive payoff below a 5PN approximation. Nonetheless, extended body models up to 3PN have been developed. This is typically done by choosing two surfaces at a radius of about 1/3 of the separation between the inspiralling bodies (Futamase 2007). The predictions of these models are consistent with those of point-particle models, although the former models make a smaller range of predictions, and the predictions are at a lower order of approximation and accuracy; more crucially, the PN models with extended sources are not able to predict observable gravitational waves. What these models do is provide some reason to believe that the point-particle idealization is eliminable from higher-order PN models.

By contrast, EFT models do not satisfy GER and are not serious contenders to support explanations of gravitational waves. I do not provide a conclusive argument against the possibility of explanatory EFT models in gravitational physics—but I hope to show that the prospects look to be very dim indeed. First and foremost, point particles are essential to EFT models, yet physically impossible in GR. Here, the disanalogy with particle physics could not be starker. In particle physics, the point particle assumption is entirely justified as a direct consequence of taking a field-operator approach to systems with an infinite number of degrees of freedom in a quantum theory. Moreover, plausible physical interpretations of the global theory of particle physics, the standard model, include point particles. By contrast, we have seen that point particles are physically impossible according to general relativity. According to GER, if the point-particle assumption were required to construct local models that predict gravitational wave phenomena, then these local models could not be explanatory in the context of GR. EFT models are just that: local models that make essential and ineliminable use of the point particle idealization.

Point particles are not the only physically impossible assumptions in EFT models of GR. EFT models of inspiral systems, while classical, make some quantum-looking assumptions. These include wave-particle duality, specifically that the gravitational wave is also a graviton particle, and that this classical particle has quantum spin. EFT models also use the imaginary part of the effective action to make predictions about observables (the far-zone power detectable on earth), again a technique that makes sense in the context of QFT but is unmotivated in this classical context (Appendix B). These quantum-like features, essential to EFT models, are physically impossible in the classical theory of GR (keep in mind that these are not models of quantum gravity!).

The EFT approach to inspiral systems, and EFT models in GR more generally, have several virtues, foremost among which is their calculational efficiency. The EFT approach is a powerful way to obtain accurate predictions based on an effective action and a few renormalization coefficients at the body scale. Furthermore, it may be that EFT models become predictively superior to traditional PN models and make reliably accurate predictions beyond the calculational reach of PN models. One may even speculate that there will be heuristic benefits to EFT models, as they may lead to advances in quantum gravity models that would not have been possible following post-Newtonian methods. Whatever the further merits of EFT models, the point here is that they cannot underwrite explanations of gravitational phenomena in GR.

I have argued that PN models can explain gravitational wave observables and EFT models cannot. A key assumption of the argument is what I have dubbed GER: a necessary condition for explanation via idealized models is that no entity of the model that is essential to the explanation be physically impossible according to the relevant global theory. This section develops and defends GER.

Consider two types of requirements that a scientific explanation may satisfy. Local requirements have to do with characteristics of the explanans and the relation between the explanans and the explanandum. Carl Hempel’s deductive-nomological account, for instance, requires that the explanandum be entailed by the explanans, that the explanans contain a law statement, and that the statements in the explanans be true (Hempel 1965). Causal accounts of explanation may require that the explanans describe the relevant micro-causal history of the explanandum (Salmon 1984) or answer what-if-thing-had-been-different questions (Woodward 2003).

Global requirements concern the relation between the explanation and the larger scientific field in which it is embedded. These are features external to the explanation itself. Philip Kitcher’s account of explanatory unification puts global requirements front-and-centre: a particular argument is explanatory only if it is appropriately connected to a global theory that itself has explanatory power. For Kitcher, what gives a global theory explanatory power is simple: unification. The “appropriate connection” here is also simple: law statements featuring in the explanans must be identical with, deductively derivable from, or straightfoward approximations of global theory (Kitcher 1989, pp. 452–454).

Causal approaches to scientific explanation often ignore global requirements (Wayne 2015). Salmon and Woodward, for instance, develop accounts of causal explanation entirely in terms of local features of the explanation itself: the appeal to relevant causal facts in the explanandum; the truth of the explanans and explanandum, and the causal relation between the phenomena described in the explanans and the explanandum. Nothing more would seem to be needed to characterize successful explanation in science. In the context of these traditional approaches to explanation, global requirements may seem otiose.

All this changes when we focus on how scientific explanation functions using local, highly idealized models in science. As we have seen, derivations of gravitational waves in GR appeal to local PN or EFT models. They do not include of the laws of the global theory, the EFEs; they do not include laws deductively derivable from the EFEs; and they do not even include straightforward approximations of the EFEs. Rather, gravitational-wave predictions include only statements about a highly idealized local model. An intricate set of steps is required to get from the laws of GR expressed in the EFEs to claims about the local PN or EFT model contained in the explanans. These features are characteristic of idealized-model explanations, where we know some statements in the explanans are false, because they describe objects and properties—such as point particles—that do not exist in the physical system.

The issue here is that not just any set of false statements that entail a statement qualify as explaining it. Some idealized models merely predict phenomena of interest, what scientists often call phenomenological or data models, while others also explain. An important difference between the two sorts of local models lies in their relations with the larger scientific field. For present purposes, there are two salient features of these relations. First, where there is a relevant global theory with independent explanatory power, some sort of justification by this global theory is necessary for the local model to be explanatory. Second, in the context of physics at least, a minimum threshold for this justification is that no component of the local model that is essential to the explanation be physically impossible according to the global theory. Together, these imply the global explanation requirement GER invoked in Sect. 5.

The first feature applies in cases where a scientific field is covered by an overarching theory with independent explanatory power. GR is widely considered to be a paradigm case of such a theory—well confirmed, of broad empirical scope, unified and explanatory. Now consider a local model in the scientific field that applies to a certain type of target system. The justification of the local model by global theory is a matter of degree, and it depends on the contents of the model and the connections between the two. Where the local model is a submodel of the global theory, or an approximation thereof, the justification is clear: we have good reason to believe the local model is explanatory because it is a straightforward application of the theory to this particular type of target system. For idealized models, we have seen that the connections are more complex. The pathways from global theory to local model involve procedures such as abstractions, singular perturbation methods, and contrary-to-fact assumptions. These pathways are not contained within the global theory, and the global theory does not provide an algorithm for constructing local models for specific target systems. Nonetheless, these pathways may provide justification for the local model.

A minimum threshold for justification is required in order for a local model to support explanations in a field with a global theory. A local model which is completely disconnected from the relevant global theory may be predictive, but not explanatory. For example, we do not consider a creation-science model of the origin of a species to be explanatory in the context of contemporary evolutionary biology. By contrast, a local model that is a direct application or approximation of an explanatory global theory to a specific target system will be explanatory, the way Newtonian models can explain the dynamics of small-scale, slow-moving physical systems in the context of GR. The interesting space is between these two extremes. Where does the threshold for justification lie?

In the context of physics, I contend, the minimum threshold for justification is that no component of the local model that is essential to the explanation be physically impossible according to the global theory. As we have seen, a physically impossible idealization is one which is inconsistent with the dynamic and synchronic constraints imposed by the laws of the relevant global theory. To say that a component is essential to a model means that that we have good reason to believe that the component cannot be eliminated from this kind of model for target systems of this kind.

To motivate this threshold for justification, consider the case in which it fails to hold. Here, physically impossible entities are essential to making predictions about target phenomena, and these predictions are taken to be explanatory. For idealized models—models which do not accurately represent aspects of the target system—the immediate consequence is that anything explains anything. On traditional accounts of explanation, local requirements on the explanans, such as its truth or causal content, may be sufficient to set a substantive bar for explanation in the absence of any connection with global theory. Those local requirements do not apply to idealized models, and so a philosophical account of explanation will lack normative force without a threshold for justification by global theory. There is simply no way to exclude even the most outlandish, physically impossible entity or dependency relation from putatively explaining physical phenomena in a system that falls under an explanatory global theory. The minimum threshold for justification by global theory proposed here sets a reasonable lower bar for explanation via idealized models in physics. As I have argued elsewhere, neglecting this threshold—and neglecting global requirements more generally—is a significant weakness of several recent model-based accounts of explanation (Wayne 2017).

In explanations of inspiral systems in GR, physicists have never claimed EFT models to be explanatory of gravitational waves, to the best of my knowledge. Since Goldberger first proposed EFT models of gravitational waves, they have been put forward as phenomenological models with great calculational and predictive virtues, but lacking adequate justification by GR. By contrast, the explanatory virtues of post-Newtonian models have been widely touted since these models were first developed by Einstein. Indeed, his very first post-Newtonian model correctly predicted the precession of the perihelion in Mercury’s orbit, and this was universally accepted as a general-relativistic explanation of the phenomenon. Clearly, scientists judge that PN models are justified by GR, and therefore explanatory, in a way that EFT models are not. Physicists’ own appeal to global theory when assessing the explanatory merits of idealized local models supports the idea that a successful account of idealized-model explanation needs to include a requirement that the local model be justified in some way by the global theory. Moreover, the match between the physicists’ considered judgments of explanatory power and GER provides additional support for GER.

We have seen that PN models are constructed based on solutions of the fundamental equations of motion of general relativity, the EFEs. While these are not regular perturbative solutions, there is a reasonably strong theoretical justification of the model-construction methods. As well, the near-zone component of the PN model is an approximate representation of the near-zone target system in many respects, e.g., it models the spacetime manifold with a definite metric. I have argued that even though accurate higher-order PN derivations of gravitational waves have been available since the mid-1980s, only since the development of extended-body PN models in the mid-2000s has the point-particle idealization been partially discharged such that these predictions are also potential explanations of observable gravitational phenomena.

The fact that the point-particle assumption is probably eliminable at higher orders distinguishes PN models from other sorts of infinite idealizations, such as thermodynamic models at criticality, semi-classical models of quantum phenomena, and models with infinite population sizes in genetics and economics. If there is a broader lesson to be learned from considering explanatory practices in contemporary physics—and given a pluralist approach to scientific explanation, this is a very big if—it is that models invoking ineliminable infinite idealizations cannot have explanatory power.