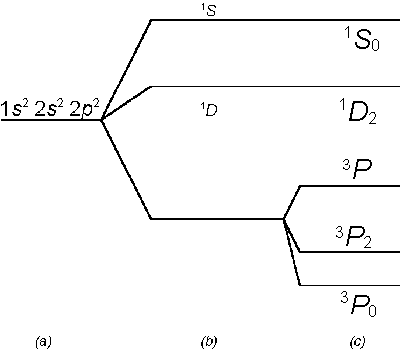
Figure 1: Energy levels in the ground state of carbon, after Cartwright (1983: 67).[17]
Cartwright attempts to argue from an analysis of the composition of forces, and more generally the composition of laws, to the conclusion that laws must be regarded as false. A response to Cartwright is developed which contends that properly understood composition poses no threat to the truth of laws, even though agreeing with Cartwright that laws do not satisfy the ‘facticity’ requirement. My analysis draws especially on the work of Creary, Bhaskar, Mill, and points towards a general rejection of Cartwright’s view that laws, especially fundamental laws, should be seen as false.An important argument in Cartwright (1980) proceeds from an analysis of the composition of forces to the thesis that, except in specific and unusual circumstances, fundamental laws have to be regarded as false. Her argument is criticised by Creary (1981) and Cartwright's presentation of essentially the same material in her (1983) is updated to include a response to Creary. A major foil for Cartwright's argument in both its incarnations is Mill's (1856)[2] discussion of the composition of causes, whose views are also criticised by Bhaskar (1978). Furthermore Nagel (1963) takes Russell (1903) to task for making a claim in some significant respects similar to that advanced by Cartwright.
My principal thesis in what follows is that Cartwright’s analysis of composition is seriously flawed, and that it poses no significant obstacle to the interpretation of fundamental laws as true. My rejection of her position is not comprehensive, since I do not propose to defend what she calls the ‘facticity’ account of laws, which holds that true laws state the facts about actual outcomes. Nonetheless, holding short of the facticity view need not mean going so far as to hold that fundamental laws are lies.
Since I want to defend fundamental laws, Cartwright’s treatment of composition is especially important for my purposes. Recall her admission (e.g. 1983: 77) that a fundamental law can be regarded true when it does ‘state the facts’. It seems more than plausible (although this is exactly what Cartwright denies) to regard at least some situations, traditionally dealt with by means of composition of forces, as being characterised by more than one law being true of them. So, if the conclusion to her treatment of composition can be blocked, it points the way to a relatively general rejection of aspects of her anti-fundamentalist stance, in defence of a position committed to the general truth of at least some laws, but not to the excesses of the facticity interpretation. What is at stake in the debate over composition is the question of what we are entitled to say we know is the case where more than one causal law, tendency or capacity is at work. An argument which takes Cartwright’s admission that fundamental laws can sometimes be true, and develops a suitable truth-preserving account of composition, can significantly extend the scope of fundamental physical laws in the face of Cartwright’s patchwork realism.[3] I believe that just such an argument can be constructed, blocking Cartwright’s anti-fundamentalist conclusion, and drawing for the most part of Bhaskar and Mill,[4] although also making use of Nagel’s criticism of Russell, and Creary’s of Cartwright. The laws which I will discuss are examples used by Cartwright herself, especially Newton’s and Coulomb’s laws. It is not important for my argument that Newton’s, for example, is regarded as an approximation from the point of view of special and general relativity. The reason for this is that such arguments concern the potentially superior credentials of even more general fundamental laws, rather than the propriety of reasoning with fundamental laws at all. If Newton’s laws are to be criticised on relativistic grounds, in the spirit of correction and improvement, they need to be defended from Cartwright first. I begin with Cartwright’s (1980) account of the issues.
Cartwright’s argument, briefly, is (a) that laws must either satisfy the facticity requirement (i.e. ‘state the facts’) or be false, (b) that where more than one law combines neither of them satisfies this requirement, and hence that (c) in such cases both laws are false. The key premise here, as I see it, is (a), the ‘facticity or falsehood’ dilemma. As noted already, Cartwright’s foil is, to some extent, Mill’s account of the composition of causes. On Mill’s view, in cases where composition takes a mechanical[5] form, both (or all) of the laws in play have their full effect:
If a physical body is propelled in two directions by two forces, one tending to drive it to the north and the other to the east, it is caused to move in a given time exactly as far in both directions as the two forces would have separately carried it; and is left precisely where it would have arrived if it had been acted upon first by one of the two forces, and afterwards by the other (1973: 370-1).Mill makes the same point by saying that ‘even when the concurrent causes annihilate each other’s effects, each exerts its full efficacy according to its own law, its unique law as a separate agent’, and that a key characteristic of conformity to the principle of the composition of causes is that some laws (one of Mill’s examples is the conservation of ‘weight’) are ‘rigidly fulfilled in every combination into which the objects enter’ (1973: 373). Mill regards the final effect of these cases as being the sum of the effects of the laws taken separately, and takes the parallelogram law in mechanics as the model for addition in the mechanical case. There is a risk of ambiguity in Mill’s description here, since at times he speaks of causes ‘annihilating’ one another’s effects while still having full ‘efficacy’, and at others he maintains that both laws have their full effects. Neither of these possibilities, though, is the same as what Cartwright seems to be taking Mill as saying, which is that the actual outcomes which would have obtained were each law to operate in isolation must actually take place for the law to be considered as having its full effect. We will see shortly how this interpretation affects both Cartwright’s reading of Mill, and of the wider issues at stake here.
A paradigmatic example of composition along the lines presently under discussion is that given by Newton. His parallelogram rule of composition is presented as a corollary to his three laws of motion, to the effect that:
A body, acted on by two forces simultaneously, will describe the diagonal of a parallelogram in the same time as it would describe the sides by those forces separately (1934: 14).This is supposed to follow for the most part from Newton’s second law, the law that changes of motion (accelerations) occur in the direction of the impressed force, and the first law, that motions persist with unchanging direction and speed unless forces are applied. Newton’s geometrical reasoning is straightforward enough. Given a body starting at point A, and two forces where the one, M, would drive the body along a line AB to point B in some time, while the second, N, would drive it along the line AC to C in the same time:
… let the parallelogram ABCD be completed, and, by both forces acting together, [the body] will in the same time be carried in the diagonal from A to D. For since the force N acts in the direction of the line AC, parallel to BD, this force (by the second Law) will not at all alter the velocity generated by the other force M, by which the body is carried towards the line BD. The body, therefore, will arrive at the line BD at the same time, whether the force N be impressed or not; and therefore at the end of that time it will be found somewhere in the line BD. By the same argument, at the end of the same time it will be found somewhere in the line CD. Therefore it will be found in the point D, where both lines meet. But it will move in a right line from A to D, by Law I (1934: 14).Newton’s position, then, is that each force individually determines a range of possible outcomes, and that the combined affect of several forces will be the outcome at which the relevant ranges intersect. It should be clear that the case of two forces in equilibrium is a limiting case where the body acquires no change in motion, since there is no net force, and that the case where two or more forces act in the same direction is another limiting case, where the sole effect of combination is a change in the magnitude of the acceleration due to either force alone.[6]
Cartwright herself takes a Newtonian law, the universal law of gravitation as her starting point, noting that Feynman endorses the evaluation of it as ‘the greatest generalization achieved by the human mind’ (Feynman 1965: 14, in Cartwright 1980: 76).[7] It is precisely this notion of the generality of Newton’s or any other law which Cartwright rejects. As we would express the law now, it reads:
F = Gmm´/r2Alternatively, in Feynman’s words (also quoted by Cartwright):
The Law of Gravitation is that two bodies exert a force between each other which varies inversely as the square of the distance between them, and directly as the product of their masses (Feynman 1965: 14, Cartwright 1980: 77).It should hardly need pointing out that this law says, by itself, nothing at all about what will actually happen to the bodies in question. The same goes for Coulomb’s law, which Cartwright brings into the discussion shortly. What each law does say is that a force will be exerted, which is not the same thing as saying what will happen at all. Granted, Newton’s second law holds that a given body will accelerate in the direction of the (net) force upon it, so there are some laws which do make claims about what will happen. The point I need to emphasise very briefly here is simply that there is no justification for setting out by holding all laws to a standard assuming that their purpose is to describe the actual flow of events, when not all of them make claims about happenings (like accelerations) at all.
Nonetheless, Cartwright asks whether this (Newton’s) law truly describes ‘how bodies behave’ and answers that it does not, noting that Feynman himself ‘gives us one reason why’ in his description of Coulomb’s law, stating the force due to electrical charge, another inverse square law. (Feynman himself does not present Coulomb’s law as an example of something which shows that the universal law of gravitation is ever false, simply as another example of a law which he regards as having great generality.) This law relates the magnitude of the force in question to the charges of the two bodies thus:
F = qq´/r2The ‘facticity or falsehood’ dichotomy, which I read as premise (a) in Cartwright’s argument, begins to show itself when she considers the case of bodies which are both massive and charged:
It’s not true that for any two bodies the force between them is given by the law of gravitation. Some bodies are charged bodies, and the force between them is not Gmm´/r2. Rather it is some resultant of this force with the electric force which Feynman refers to (1980: 77).So far so good. Cartwright, though, describes this by saying that massive bodies are ‘counterexamples’ to Coulomb’s law, and that charged ones are ‘counterexamples’ to Newton’s, concluding that ‘the two laws are not true; worse, they are not even approximately true’ (1980: 77). I argue shortly that Cartwright’s case has gone entirely off the rails by this early point, but not for the reasons she proposes when she notes that there is a possible rejoinder which could be put here, to the effect that she has not formulated the laws correctly, and that, allowing for the existence of ‘implicit ceteris paribus’ modifiers, Newton’s law should be taken to read something more like:
If there are no forces other than gravitational forces at work, then two bodies exert a force between each other which varies inversely as the square of the distance between them, and varies directly as the product of their masses (1980: 77).Cartwright is prepared to allow that this law is a true law ‘or at least one held true within a given theory’, but objects that it is not ‘very useful’ because it can explain only ‘very simple ideal circumstances’, that is, cases where only gravity is ‘at work’ (1980: 77). Cartwright notes at once, though, that real explanations, directed at complex circumstances, often break the phenomenon in question down into simple parts, and that one version of this type of explanation is what Mill called explanation by composition of causes (Cartwright 1980: 78). A paradigm of this type of explanation is vector addition, and Cartwright asks whether vector addition provides a ‘simple and obvious answer’ (1980: 78) to her concerns, but replies that it does not. On the vector addition view the forces due to gravity and to charge would both be present, and the net force or resultant determine what acceleration would ensue, in the absence of other factors. Cartwright responds as follows:
The vector addition story is, I admit, a nice one. But it is just a metaphor. We add forces (or the numbers that represent forces) when we do calculations. Nature does not “add” forces. For the “component” forces are not there, in any but a metaphorical sense, to be added; and the laws which say they are must also be given a metaphorical reading (1980: 78).In explanation for this bold assertion Cartwright maintains again that in cases where both charge and gravity are in play the forces due to gravity and charge are ‘not real, occurent forces’, that in interaction ‘a single force occurs – the force we call the “resultant” – and this force is neither the force due to gravity nor the electric force’ (1980: 79). Noting that Mill would reject this claim, and quoting his description of the body simultaneously propelled with equal force in two directions, north and east (quoted above, Mill 1972: 370-371) Cartwright objects that while events may have temporal parts, they cannot have parts of the sorts described by Mill, that ‘no pure north motion can be part of a motion which always heads northeast’ (1980: 79). This is not an argument but an assertion, although Cartwright does say, without explanation, that ‘We learn this from Judy Jarvis Thomson’s Acts and Other Events’ (Cartwright 1980: 79, 1983: 61) but gives no specific reference. I turn to this and the parts and sums question shortly. Pushing the ‘facticity or falsehood’ dichotomy again, Cartwright urges:
In the simplest case, the consequences that the laws prescribe must be exactly the same in interaction, as the consequences that would obtain if the law were operating alone. But then, what the law states cannot literally be true, for the consequences that would occur if it acted alone are not the consequences that actually occur when it acts in combination (1980: 83, 1983: 72).Saying again that it is ‘implausible’ to regard the separate forces as parts of the net or resultant force, Cartwright does say that we can preserve the truth of the laws ‘by making them about something other than the facts’, that is ‘the causal powers that bodies have’ (1980: 79). This view sounds close to Bhaskar’s (e.g. 1978: 98-105). Having raised it, though, Cartwright immediately abandons it, saying that the task of giving an account of causal powers seems very difficult, and that ‘no story I know about causal powers makes a very good start’ (1980: 79, 1983: 61). [8] Making the laws be about powers without saying when or whether they will be exercised only adds to the explanatory task rather than solving it, since it leaves us having to explain how it comes to be that the powers are exercised in any given case. Making the laws be about regularly exercised powers, though, is to take the Bhaskarian (1978: 91f) step of making them attributions of tendencies, which is to keep them as a kind of law. I return to this point towards the end of this paper.
There are a number of things which need to be separated carefully here. It is beyond dispute that Cartwright is correct in maintaining that except in unusual and often controlled conditions the laws of physics do not satisfy the facticity requirement. Whether that makes those laws false (or ‘lies’), and especially whether it does so in the present case of force laws, is another matter. A further important question is whether Cartwright’s proposed solution, i.e. making the laws be about causal powers can be made to work without either some kind of realism about the component forces or the retention of other factors in the traditional account.
I propose that rather than asking whether the laws of physics state the facts, we should ask what kind of facts it is that they do state. Even though the laws only rarely, or in particular conditions, enable us to accurately describe the actual course of events, I maintain that they can be regarded as stating truths about what is happening. Furthermore I will argue that Cartwright’s talk of causal powers, and her more recent talk of capacities, is best cashed out in terms of just the notion of laws, especially fundamental laws, which she wants to deny. I approach the issues by means of some of the existing responses to Cartwright, and her rejoinders.
Creary (1981) has offered a criticism of Cartwright (1980) which attempts to salvage some facticity for fundamental laws. He regards the key step in Cartwright’s argument as the premise that the ‘laws used in explanation by composition of causes do not describe truly how the relevant things behave or what they do’ (1981: 148) a premise which he argues is false. Joining the debate with Cartwright’s example of the two massive and charged bodies, he contends that the account of the explanatory force of fundamental laws Cartwright entertains briefly following her rejection of their claim to truth and of the traditional account of composition, is ‘woefully inadequate’, quoting the following important passage:
... the law of gravitation claims that two bodies have the power to produce a force of size Gmm´/r2. But they don’t always succeed in the exercise of it. [...] ... the laws we use talk not about what bodies do, but about what powers they possess (Cartwright 1980: 79, in Creary 1981: 150).Creary argues that this approach is a ‘non-starter’ for the reason that what we need in an explanation of the motions of the particles under consideration is a view about powers which are exercised, rather than simply possessed, if we are to be able to have any significant grip on what the particles do in fact do. In Bhaskar’s (1977: 91f) terms we could say that what is needed is a way of thinking of things which can cope with the idea of a power exercised without being actualised. Unexercised powers don’t explain much. Creary proposes that a ‘facticity-preserving solution’ is possible, though, which relies on a distinction between laws of causal influence and laws of causal action (Creary 1981: 150-151). The distinction works by making the force laws into laws of causal influence, which are to be read factually as saying that certain forces are exerted in certain conditions, but where what actually happens in a given situation depends on the laws of causal action, which determine how the various causal influences will work together. There is, prima facie, a lot to recommend this view, since as noted already force laws do not by themselves make any claims at all about what will happen, stating only that under certain conditions certain forces will be exerted. Creary wants to take these laws at face value, and to keep separate the question what will happen when forces are exerted, especially in combination. So, on Creary’s view, Newton’s first, second and third laws should be seen as laws of causal action, while his law of gravitation is a law of causal influence.[9]
On the basis of this distinction Creary opposes Cartwright’s anti-realism about component forces in favour of the reality of the resultant. Creary inverts the priority, arguing that it is preferable to regard the component forces as real or ‘natural’, since they are related to our well-justified knowledge of the laws of causal influence, while the resultant is the fiction, the ‘mathematical’ component force (1981: 151-2). Creary also notes, correctly that Cartwright offers no direct argument in favour of her anti-realism about the component forces, but rather offers an attempted refutation of a single alternative view, based on considerations of the part-whole relation.
Creary makes clear that on his own view, where the component forces are real because they are the influences of real causes, ‘causal influences are neither causes nor effects, but constitute a distinct third kind of entity in the causal ontology, that mediates between causes and their effects’ and argues that this approach to causal influences is essential ‘to their role in grounding the facticity of the laws of influence that figure so prominently in [...] explanations by composition of causes’ (1981: 152). This is in direct opposition to Cartwright’s view, which is that effects cannot typically be decomposed into parts, or seen as the sums of various partial causes. Creary maintains that his view, where the causal influences are an intermediate step, solves the problem of getting from cause to effect. It does this, he claims, by making forces independent of both the conditions under which they arise, and the outcomes to which they give rise, so that we can reason from situations to forces and thence to outcomes, although the final step will only be possible where we have suitable laws of causal action.
One final point in connection with Creary’s proposal is that although he takes vector addition as a paradigm case of a law of action, he is also careful to note that not all composition or combination may take that form, and argues that the key requirement from the notion of laws of action is that ‘it makes sense in general to speak of reinforcement, interference, and predomination occurring among the causal influences governed’ by the laws of action (1981: 153). The key point, though, is that we do not need to know these laws in advance in order to salvage the laws of causal influence.
Unsurprisingly Cartwright is having very little of this. In the section added to the (1983) version of ‘Do the Laws of Physics State the Facts?’ she raises two objections to Creary’s argument. The first is that there are rarely any general laws of interaction which might do the work done for Creary by vector addition in his account of the gravity-charge example, and that without such general laws ‘the collection of fundamental laws loses the generality of application which Creary’s proposal hoped to secure’ (1983: 63). Cartwright goes on to discuss the use of models and approximations in the study of flow processes, illustrating how a variety of different models are used in a pragmatic manner, taking this to show further the irrelevance of fundamental laws. This line of objection to Creary does not do any significant damage,[10] for two reasons. Firstly Creary’s view in no way depends upon the availability of laws of causal influence, and as noted he himself recognises that such laws may be unknown, difficult to apply and so forth. Secondly the ‘generality of application’ Creary was after has to do with the laws being true as laws of causal influence, which by itself carries no automatic implication that they could play any role in prediction or modelling. It is entirely consistent with Creary’s view that phenomenological laws could be more accurate and useful in most situations. Cartwright’s first objection simply fails to hit the mark.
Cartwright’s second objection is directly aimed at Creary’s talk of causal influences. Cartwright points out that she and Creary disagree about the reality of the component forces: she wants the resultant only, and he the components. She notes that in the case of composing forces Creary’s approach of placing the causal influence ‘between the cause and what initially looked to be the effect’ is ‘plausible’ (1983: 66), but argues that this way of doing things will not make for a reasonable general strategy for explanation:
Take any arbitrary example of the composition of causes: two laws, where each accurately dictates what will happen when it operates in isolation, say ‘C causes E’ and ‘C? causes E?’; but where C and C' in combination produce some different effect E''. If we do not want to assume that all three effects — E, E', E'' — occur (as we would if we thought that E and E', were parts of E''), then on Creary’s proposal we must postulate some further occurrences F and F', as the proper effects of our two laws, effects that get combined by a law to yield E'' at the end (1980: 66).This does not seem to be getting anywhere, since Cartwright is simply repeating her position rather than offering any new arguments in defence of it. What is at stake here is Creary’s proposal concerning a way of thinking about composition of forces where the causal influences are not identified with their effects, but with their production of certain tendencies. Cartwright’s response, just quoted, is framed entirely in terms of a way of seeing things where laws are identified with their effects, which is how it is that she ends up with the worry about all three effects being real. It does not help that Cartwright aims to reject the facticity view, the point is that Creary’s proposal is neither the facticity view nor Cartwright’s own, which means that simply repeating anti-facticity arguments is not a proper response to Creary at all. In order to make any progress we need to get away from the current deadlock. To do this it is not necessary directly to refute Cartwright’s argument; developing a satisfactory account of composition which saves fundamental laws and is immune to her lines of criticism will be sufficient. Bhaskar and Mill show the way to just such an account. After looking at their views I say something more about the question of parts and wholes, Cartwright’s remarks on which are generating more heat than illumination here, and finally at some arguments Mill offers in favour of laws of maximal generality.
How are we best to think of cases where more than one causal influence is at work? I propose to take it as a premise that given some grounds to think that a causal law is true based on the examination of cases where that law acts in isolation we have a good prima facie reason to think that the same law obtains in relevantly similar cases where either there are other known causally relevant factors or the actual outcomes do not conform to those predicted by the original law taken alone. This is to say, for example, that an experiment on the behaviour of massive bodies is something I will interpret as an experiment which tells, to the extent that it is successful, us about mass in general, rather than the masses of just those bodies which are involved, or about what happens to masses when just that happens to them. The test here, then, is to see if this premise stands up in the face of the composition problem. Taking, to stay with Cartwright’s example, Newton’s law of gravitation as a truth about bodies with masses in general and Coulomb’s law as a truth about bodies with charges in general, how do we deal with the case where we are considering a pair of bodies which are both massive and charged?
Bhaskar thinks that there are two mistakes which need to be avoided here. As noted his view is that laws of nature should be regarded as typically being not nomic, that is not statements about what happens, but rather ‘normic’, that is statements of tendencies or the ways of acting of things. So he rejects Mill’s contention that where two or more laws interact in a way which leads to a result unlike that predicted by either, ‘all are fulfilled’ (Mill: 1973: 443) saying that ‘Mill’s mistake here is to suppose that whenever a tendency is set in motion the effect must be in some sense ... occurring...’ (1975: 99).[11] But Bhaskar also rejects the view, which he attributes to Geach,[12] of ‘supposing that whenever no effect (of a given type) occurs, nothing can be in motion or really going on’ (1975: 99). Quite correctly Bhaskar points out that the view he attributes to Geach is simply wrong, that ‘Balaam’s ass is pulled two ways; we do just manage to keep our tempers’ (1975: 99-100).[13]
A crucial aspect of Bhaskar’s treatment of tendencies is that they may be exercised unfulfilled. When this happens, he maintains that there are two things which need not be doubted:
[…] (a) that something actually happens, towards explaining which the exercise of the tendency goes some way; and (b) that something is really going on, i.e. there is a real generative mechanism at work, which accounts for the influence of the factor the tendency represents in the generation of the event (175: 99).From Bhaskar’s point of view both mistakes are versions of the same fundamental error: that of ‘seeing the fulfilment of a tendency [as] a condition of its exercise’ (1975: 100) which in Mill’s case results in thinking of both tendencies as being actualised, and in Geach’s in regarding neither of them as in play at all. The missing distinction is that which Bhaskar draws between the exercise and the fulfilment of a tendency. A tendency or power may be present unexercised, so that it ‘remains true to say of a Boeing 727 that it … has the power to … fly at 600 m.p.h. even if it is safely locked up in its hangar’ (Bhaskar 1975: 87). Similarly a power may be exercised un-actualised: the aspirin may do whatever it does, and yet my headache persist.
It is instructive to consider cases of equilibrium, when in a clear sense the outcome is that nothing happens. With a nil resultant, and given Cartwright’s anti-realism about component forces we would be forced to say that no forces at all are in play. This, though, would make it very difficult for us to say what is going on, especially if we consider related but only slightly changed situations. To keep consistency with the above example let us imagine a body both massive and charged, such that it is suspended, stationary, above the ground. That is to say, on the view I am attempting to save, that it is subject to two forces which balance out so as to result in no acceleration. Our understanding of Newton’s law gives us to expect that it will be subject to a downwards force of a given magnitude. Our understanding of Coulomb’s law gives us to expect an equal force in the opposite direction. The body, as noted, ‘does nothing’, so the ‘resultant’ on Cartwright’s view and on views closer to Creary’s or Mill’s is nil. But for Creary, Mill and any realist about components the fact that the resultant has zero magnitude explains the fact that nothing happens: the forces balance out. For Cartwright there are no forces here at all, and no explanation seems possible.
Viewing these laws (Newton’s and Coulomb’s) as force laws, which is what they look like anyway, supplemented by the notion of composition enables us to take the laws as true without committing ourselves to the excesses of the facticity view. We can say what the difference is between cases where the laws do enable prediction and those where they do not, and make sense of reinforcement, counteraction, equilibrium and other consequences of multiple tendencies being in play. The difference, briefly, is that it is only in some cases that we know how to work with a multitude of influences which may be reinforcing and counteracting one another.[14] Contra Cartwright the outcomes of situations where more than one law are is play is not a counterexample (Cartwright 1980: 77) to either law, but an instance of its operation, which need not be identified with its effects. The burden of argument here is now even more clearly with the Cartwrightian, who has no independent argument for the unreality of the component forces. There is, though, the matter of what Cartwright says about sums and parts.
Cartwright insists repeatedly, although without any real justification, that vector components cannot be parts of vector sums, at least where the vectors represent forces, motions and perhaps other physical factors. On her view, as noted, ‘no pure north motion can be part of a motion which always heads northeast’ (1980: 79). The closest she gets to actually defending this view is her claim that ‘we learn this from Judy Jarvis Thomson’s Acts and Other Events’ (Cartwright 1980: 79, 1983: 61). This is not an argument, and in any event does not seem to be true. Thomson (1977) is a work about actions and events, and, in large measure, about the question of how best to think of parts of events. Thomson’s main concern is with events which have temporal parts: consider a shooting which brings about a death after some delay. Is the whole process a killing? Is the shooting then identical with the killing itself, or a part of the killing? Thomson defends the thesis that events can have temporal parts, as long as the part ‘plays a role’ in the event of which it is a part (1977: 60). Thomson just does not argue that events cannot have spatial parts.[15]
Cartwright’s concern here, though, is similar to one which vexed Russell (1903: 477) who considered a case in which there are three particles A, B and C, with B and C both exerting a force on A, and we would normally expect the resultant force to be the vector sum of each separate force. Russell objects as follows:
But this composition is not truly addition, for the components are not parts of the resultant. The resultant is a new term, as simple as their components, and not by any means their sum. Thus the effects attributed to B and C are never produced, but a third term different from either is produced. […] Thus we reach an antinomy: the whole has no effect except what results from the effects of the parts, but the effects of the parts are non-existent.This is close to Cartwright’s view, although she does not express it as an antinomy. Nagel (1963) objects against Russell that he is operating with a needlessly restrictive notion of ‘sum’, for which, furthermore, he has given no justification. Nagel contends that ‘no antinomy arises from the supposition that, on the one hand, the effect which each component force would produce were it to act alone does not exist, while on the other hand the actual effects produced by the joint action of the components is the resultant of their partial effects’ (1963: 142). From Nagel’s point of view the ‘sum’ of more than one thing of some kind will not necessarily have the constituents as literal parts, as is the case with length, but will more generally be determined by some function.[16] What function exactly applies in any type of case will be an empirical question on Nagel’s view, and he makes clear that the history of science teaches us to expect some variety: not all addition is linear, not all retains the added elements as proper parts, etc. Cartwright’s demand that the parts be present in the sum is like the demand of a customer that a withdrawal from her bank account comprise the actual notes and coins that she originally deposited.
Not only that, forces have direction and magnitude, and can thus unproblematically be represented by vectors. The standard operations for adding vectors work perfectly well in at least some cases where the vectors are forces: Millikan’s experiments to determine the charge on a single electron, the calculation of where a satellite or spacecraft will go under the influence of both its own engines and gravity, Coulomb’s own experiments on the force due to charge, the paths of projectiles, powered flight, and so-on. But all of these are cases which fall in areas where Cartwright urges us to regard the laws as false, since they do not meet the requirements of the facticity view. That is to say, already, that there is more than good enough reason to regard the scope of laws as extending some of the way beyond what Cartwright allows. Furthermore, it would be unacceptably ad hoc to limit the validity of the laws at this point. Newton’s law is a law about masses – we know that it holds more than well enough when we have isolated gravity from other influences, and we also know that in some other cases where other forces are in play, it holds too. We have no reason to believe that masses other than those we have examined, or masses in configurations other than those we can compute, are different qua masses. So the responsible conclusion is that the law holds, but we are uncertain how to apply it, or how to factor in the other influences. To say that the law cannot apply because we cannot do the sums, or because other factors will make the outcome different to what it would be if the law acted alone is to get the epistemological cart before the ontological horse.
Cartwright says she does not know why there are tracks in a bubble chamber unless there are electrons in the chamber (1983: 92). In the light of what has been said here I can reply that I don’t know how we know the charge on electrons (so that we can say what they would do in a bubble chamber) at all unless we can compose forces.
There is one further argument to be made here and it has already been made by Mill. Fundamental laws have been salvaged at the expense of arguing that the kind of facts which they state are ones which only rarely permit predictions. This may make it seem as though they are, even if possible candidates for truth, a poor substitute for empirically accurate phenomenological laws. Granting the predictive power and usefulness of phenomenological laws, though, does not mean relinquishing any sense of the value of the fundamental variety.
Mill argues, in fact, that the most general formulation of a law is, from one point of view, always the best. If his arguments are correct then we can also head off the simulacrum account of explanation, with a defence of the possibility of fundamental laws explaining in virtue of being true. He points out that all ‘laws of causation are liable to be counteracted or frustrated’ and hence that a law which ‘embraces a greater number of instances’ will be more likely to hold in any cases at all than one which does not (Mill 1973: 466). In a passage almost designed for the present discussion Mill presses the point by arguing that:
The same causes, acting according to the same laws, and differing only in the proportions in which they are combined, often produce effects which differ not merely in quantity but in kind (Mill 1973: 468)What he has in mind here is the application of Newton’s laws to celestial motions. Kepler’s laws are fairly good for planetary motions, and Newton’s more accurate laws approximate their predictions, while Newton himself used Kepler’s in the course of developing his own. But Newton’s also apply to bodies which do not travel in elliptical paths, from comets to cricket balls. What is different in these other cases is not the nature of motion, or the manner of acting of masses, but the particular configurations and conditions:
The law, in short, of each of the concurrent causes remains the same, however their collocations may vary; but the law of their joint effect varies with every difference in the collocations (Mill 1973: 469).That Newton’s laws explain more than Keplers’ is, then, not a matter of Newton’s being some high level simulacrum which we have no reason to take seriously beyond the limits within which those laws satisfy the facticity requirement. We know already that the laws are valid beyond the facticity requirement by examining how they hold true in cases where forces are composed. Newton’s laws explain with this range and generality because they are true, or at least far more nearly true than Kepler’s less fundamental laws of celestial motion, Galileo’s less fundamental laws of terrestrial motion, and so forth. That Newton’s laws can be placed into a different context as a result of considerations arising from the general theory of relativity is hardly an argument against the position I am defending here, which favours of laws of maximal generality.
The treatment developed here applies in cases other than those of composing forces. This is so despite the fact that in Cartwright (1980) and again in Cartwright (1983) following her discussion of Creary (1981) Cartwright discusses the energy levels in the ground state of the carbon atom with a view to showing how ‘real’ composition of causes operates in a way quite unlike that imagined by those who add vectors. Her discussion (Cartwright 1983: 67-69, following Messiah 1961) is not really a separate argument at all, though, since it crucially relies on her approach to the parts and sums question as she has already deployed it with reference to the question of vector addition.
There are, Cartwright explains, three different approaches to the problem of modelling the carbon atom (see figure 1). One (central field approximation) predicts a single energy level (a). Another counteracts the effects of an averaging step taken in the first by ‘considering the effects of a term which is equal to the difference between the exact Coulomb interaction and the average potential used in stage one’ (Cartwright 1983: 68). This results in the three levels shown at (b). The third approach takes account of the fact, ignored in the second, that the ‘internal angular momentum of the electron couples with its orbital angular momentum to create an additional potential’ (1983: 68) with the result that one of the three levels predicted by the second technique is replaced by three different levels, giving a total of five.

Figure 1: Energy levels in the ground state of carbon,
after Cartwright (1983: 67).[17]
It is clear enough where this is going: the five-level model (which Cartwright is prepared to grant is true) is a combination of several factors, some of which would, in different combinations, produce either one or three different potentials. This explains the final five levels, but Cartwright argues that we cannot regard the explanation as making use of laws, because the laws aren’t true:
But (as with the forces ‘produced by gravity’ in our earlier example) the levels that are supposed to be produced by the Coulomb potential are levels that do not occur. In actuality five levels occur, and they do not include the three levels of (b). In particular, as we can see from [the] diagram, the lowest of the three levels – the 3P – is not identical with any of the five. In the case of the composition of motions, Mill tried to see the ‘component’ effects as parts of the actual effect. But that certainly will not work here. The 3P level in (b) may be ‘split’ and hence ‘give rise to’, the 3P0, 3P1, and 3P2 levels in (c); but it is certainly not a part of any of these levels (1983: 69).There is nothing to worry the moderate fundamentalist here, though. If we assume, as Cartwright’s presentation seems to demand, that the example of energy levels is to be read as a case where several laws entailing different predictions are combined to produce a prediction unlike what either entails alone, then the five-level (c) model is unproblematically the sum of the lower level and the additional consideration of spin-orbit coupling. Start with (c) and assume that no coupling takes place (i.e. set its effect to zero) and you’ll get (b). Take (b) and add in the coupling effects and you’ll get (c). The same goes for the relationship between (a) and (b). As with vector addition it is possible to recover the parts by subtraction. The kind of addition involved is perfectly precise and rigorous, and presents difficulties only to those who want to see the literal parts present in the sum.[18]
This last point is important because it also shows that fundamental laws other than force laws can be defended against Cartwright’s line of attack. Taking the Bhaskarian line and viewing laws as tendencies in no way means restricting tendencies to forces. Although not central to my purposes here, it is worth pointing out that the notion of tendencies as laws is one which Cartwright rejects in her more recent work, but which some critics think would save her position from serious difficulties. To say that something has a power which it may or may not exercise does not explain unless we can also explain why the power was exercised in any given case. As long as we do not think of the exercise of a power in line with the facticity view, though, there is no problem with regarding fundamental powers as laws. This approach is in line with Bhaskar, and informs the criticisms of, e.g. Cartwright (1989, 1995) by Morrison (1995), Eels (1995) and Glennan (1997).
Even so, it is likely to seem as though I have been barking up an old tree here. How The Laws of Physics Lie was published in 1983, and Cartwright’s most recent book The Dappled World (1999) seems to grant much of what I am presenting here by way of criticism. So, to home in on a few particularly telling examples of this, she now reads Newton’s law of gravitation not as a statement about ‘the motions of two masses separated by a distance r, but, instead, about the force between them’ (1999: 52) and elsewhere with reference to Coulomb’s law she states that ‘the charge always ‘contributes’ the same force’ (1999: 82). In one sense the charge against me here is entirely correct, which is to say that in part my dispute with Cartwright concerns the proper use of the word ‘law’. She wants to restrict laws to regularities (or reliable probabilities), in which case we agree that there are fewer true laws than traditionally thought, and no true fundamental laws. Behind this lurks a more serious disagreement. What Cartwright calls ‘natures’ and to which she is prepared to grant some universality, though, falls short of what I am attempting to defend here.
Cartwright urges realism about capacities, and natures. Not being the kind of empiricist who would attempt to deny that, I am convinced by her arguments. But she also wants to hold on to a quite empiricist notion of law as either regularity or probability, which means that in her terms we can only say that a law applies when we have constructed a ‘nomological machine’ (1999: 49-74) which handles the ways different natures combine, when suitably isolated, to give rise to regularity or probability. I want to say ‘nothing law-like in, nothing law-like out’, that is, when one of Cartwright’s nomological machines works it does so because there are true laws going into it in the first place, and that some of these laws can be fundamental physical laws.
Cartwright is surely correct that few if any laws are remotely plausible candidates for truth if the only way laws can be true is by satisfying the facticity requirement. But there is no reason at all to think that this is the only way for a law to be true. True causal or dynamical laws express tendencies. Where only one tendency is in play, the law of that tendency can state the facts, and be true in that sense. That this is possible at all plays a very important role in the ways we discover laws. This accident of epistemology, though, in no way licences the identification of laws with their effects. Bhaskar is correct about that.
Just as tendencies can combine, so can the laws stating the tendencies. In cases where we know both the laws and the principles of composition we can do the combining ourselves, and work out what will happen. That the outcome in such cases is different to what would occur were any single tendency acting in isolation is testimony not to the falsity of the laws, but to the action of other tendencies, themselves possibly candidates for capture by true laws. There just is no argument from composition to the falsity of laws.
2
Cartwright refers to Mill (1856), i.e. to the fourth
edition of Mill’s System of Logic. My references are to the (1972)
version in the Collected Works which gives the text of the eighth
(1872) edition. There are no significant differences between the various
editions for the purposes of the discussions which occupy the present paper.
[back]
3
‘Patchwork realism’ is a term I used in Spurrett (1999)
to refer to the position defended in Cartwright (1994). Cartwright (1999)
talks of the ‘dappled world’. [back]
4
I came upon the idea of opposing Mill to Cartwright on
this point in a number of footnotes in McLaughlin (1992: 59-60, 70, 71)
which also refers sympathetically to Creary (1981). [back]
5
Cartwright’s discussion does not note that Mill held
that there were two modes of composition, although Gibbins (1984: 394)
suggests that one way of reading her position is as holding that all cases
of composition are what Mill called chemical, i.e. that no physical science
is deductive. Gibbins seems to have misconstrued Mill, though, since while
Mill did reject the thesis that chemistry (or any science where composition
occurs in the chemical mode) could be deductive on the basis of data concerning
the constituents of chemical processes, he also held that once the relevant
data about factors other than constituents was in, chemistry could become
properly deductive. [back]
6
The notion of composing motions and tendencies to motion
is older than Newton. The classical modern treatment is, perhaps, Galileo’s
account of the path of a projectile, combining a horizontal inertial tendency
and a constant downwards acceleration, and resulting in a parabolic trajectory
(see Galileo 1914: Fourth Day). Dugas (1955: 21) attributes to Aristotle
a parallelogram rule for composing motions, although the text to which
he refers, the Mechanica, is not generally regarded as the work
of Aristotle. (See Aristotle 1936: 337-9, 848b 10-30). [back]
7
It is worth noting that Cartwright has made a somewhat
bizarre choice of text to use as her target here. Feynman (1965) is a text
based on a series of popular public lectures, rather than an attempt either
to offer a philosophical account of physical laws, or to speak to a scientifically
sophisticated audience. (Cartwright’s references are to the (1967) MIT
edition, mine to the (1965) BBC edition.) [back]
8
Chalmers (1987: 91) suggests that ‘Bhaskar has made a
good start’. [back]
9
Creary’s view is closer to Mill’s than he seems aware,
a point made in McLaughlin (1992: 60), and is also similar in key respects
to Chalmers (1987: 88f). [back]
10
Gibbins is not impressed either: ‘Cartwright objects,
rather lamely I think, that one cannot always find laws of causal action
for combining casual influences.’ (1984: 395) [back]
11
There is an interpretive difficulty with Mill here, since
as Geach (in Anscombe and Geach 1973: 102-3) notes, his account combines
elements of a Humean view of causality (which is subject to Bhaskar’s criticisms
of actualism and Cartwright’s of facticity) with elements of a non-Humean
view of causality in terms tendencies, which is closer in spirit to Bhaskar
(who uses the same term) and Cartwright, whose more recent work concerns
causal capacities (e.g. Cartwright 1989). It is not important for my purposes
to resolve the exegetical problems posed by Mill’s hybrid, and possibly
contradictory treatment. [back]
12
Geach (1973: 103). It appears to me that Bhaskar is being
unfair to Geach here, since Geach’s view is actually rather close to Bhaskar’s
own. Nonetheless, whether or not Geach endorsed the thesis in question
it is mistaken. [back]
13
Bhaskar may have had Buridan’s rational ass (equidistant
between two equally attractive heaps of food, and hence subject to two
equal and opposite tendencies) in mind here. Then again, Balaam’s ass,
in the account in the book of Numbers (Chapter 22), was driven forward
by Balaam, but refused to budge since, unlike its owner, it could see the
angel blocking the road ahead. [back]
14
In her most recent (1999) book Cartwright would say that
it is only in some cases that we are able to construct a ‘nomological machine’.
Differences between Cartwright’s current position and the one I am defending
are discussed at the end of this paper. [back]
15
There is much more that could be said here about Thomson’s
analysis, which not only does not do what Cartwright says, but is also
framed in terms of a notion of causality which is far closer to the facticity
view Cartwright is rejecting than to what she is defending. Rather than
get side-tracked, though, I pursue the sums and parts question by reference
to treatments within the philosophy of science. [back]
16
In fact it can be the case that working out the
function is itself a significant scientific achievement: Consider the formulae
for adding velocities and other quantities which are central to the special
theory of relativity. Cartwright’s remarks about vector addition suggest
that in cases where velocities in the same direction are ‘added’ that no
addition takes place unless it does so in terms of Galilean relativity
rather than the special or general theory. [back]
17
Cartwright follows Messiah (1961: 703) from where she
gets her version of this figure. [back]
18
It is worth noting that Messiah himself is more than
happy with vector addition in physics. See for example (1961: 567). [back]